
Again, statistical tests can be performed to assess whether each regression coefficient is significantly different from zero.
In the multiple regression situation, b 1, for example, is the change in Y relative to a one unit change in X 1, holding all other independent variables constant (i.e., when the remaining independent variables are held at the same value or are fixed).
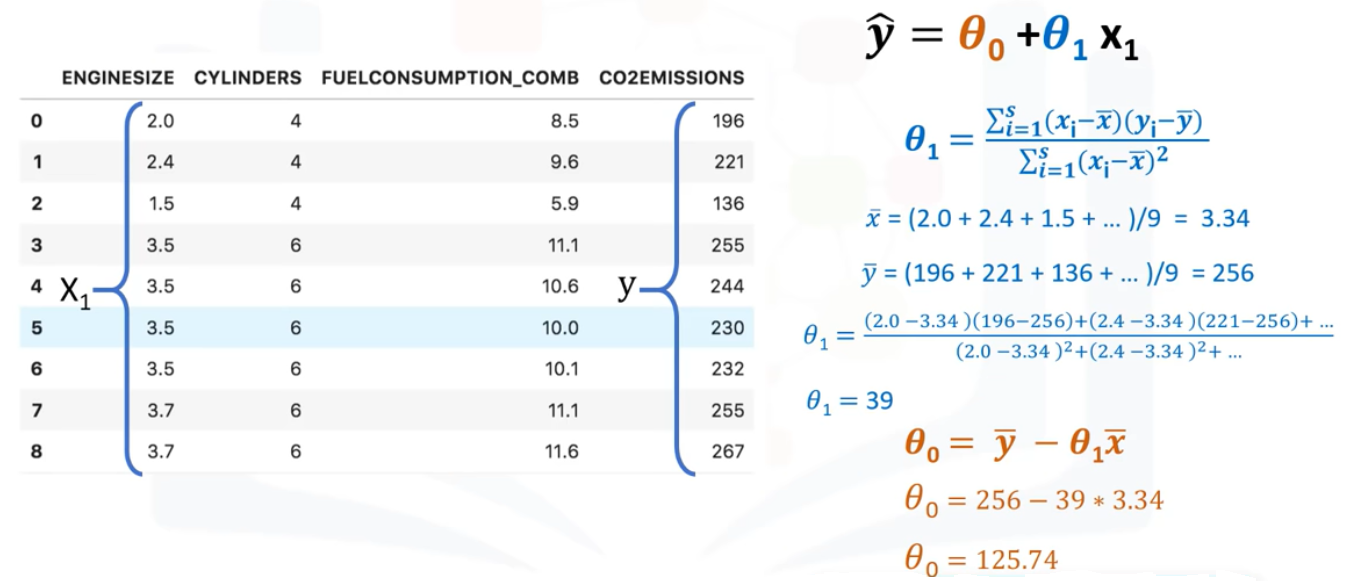
Each regression coefficient represents the change in Y relative to a one unit change in the respective independent variable. Where is the predicted or expected value of the dependent variable, X 1 through X p are p distinct independent or predictor variables, b 0 is the value of Y when all of the independent variables (X 1 through X p) are equal to zero, and b 1 through b p are the estimated regression coefficients. To estimate the mean and total of y-values, denoted as \(\mu\) and \(\tau\), one can use the linear relationship between y and known x-values.The multiple linear regression equation is as follows: In addition, if multiple auxiliary variables have a linear relationship with y, multiple regression estimates may be appropriate. The two estimates, regression, and ratio may be quite close in such cases and you can choose the one you want to use. This does not mean that the regression estimate cannot be used when the intercept is close to zero. When the auxiliary variable x is linearly related to y but does not pass through the origin, a linear regression estimator would be appropriate. Looking at the data, how will we find things that will work, or which model should we use? These are key questions. The variance for the estimators will be an important indicator.


 0 kommentar(er)
0 kommentar(er)
